Division Algebra Cyclic
This fact will be proved later. Cyclic division algebras dense lattices discriminants Hasse inv ariants maximal or ders multiple-input multiple- output MIMO ch annels multiplexing space-time b lock codes ST BCs.

Proof On Relationship Between Generators And Order Of A Cyclic Group Mathematics Stack Exchange
We consider cyclic p-algebras over F by descent from L Fµ p.
Division algebra cyclic. We generalize a theorem of Albert by showing that if µ pn L then a division algebra D of degree pn over F is a cyclic algebra iff there is d D with dpn F Fp. Examples of division algebras. Since K S contains i a primitive 4-th root of unity K S d is a cyclic extension of K S.
Let D K F γ c be a cyclic division algebra of degree n with c F 0 ie. This class still plays a major role in the theory of central simple algebras. In 20 it was shown more generally that division algebra codes are a class of codes that achieve the trade-off thanks to the non-vanishing determinant.
Let Fpbethe maximal p-extension of FWeshow that Fp has a noncyclic algebra of degree. It is shown that if D is an F-central division algebra such that charFdegD then D contains a cyclic division algebra of prime degree even though D can be a noncrossed product. If the associativity requirement is dropped there is yet another example of a division algebra over the field of real numbers.
This algebra is alternative and its dimension over is 8. Cyclic division algebras dense lattices discriminants Hasse invariants maximal orders multiple-input multiple- output MIMO channels multiplexing space-time block codes STBCs. D D 0 F 0 K for some cyclic algebra D 0 F F 0 γ c.
Hence L U G is a cyclic algebra. The first examples of division algebras that were found after the quaternions belong to the class of cyclic division algebras. Can be obtained by an explicit construction from a cyclic field extension L K.
Together with the GrunwaldWang theorem the AlbertBrauerHasseNoether theorem implies that every central simple algebra over an algebraic number field is cyclic ie. E n 1 be the canonical basis of D that is e n c e x γ x e for every x K. That the algebraic structure of cyclic division algebras was the key for constructing 2 2 non-vanishing determinant codes.
Let 1 e. Similarly L U G is a cyclic algebra and we have the desired counterexamples. 15 A sufficient condition that A be a division algebra is that a is the least power of a which is the norm of an element of Z.
Hence L U G is a cyclic algebra. Similarly L 0 G is a cyclic algebra and we have the desired counterexamplesAlbert has exhibited a non-cyclic division algebra of characteristic zero with index 4 having a pure maximal subfield. A cyclic algebra is said to be a cyclic division algebra if every nonzero element is invertible in which case we will use the notation D KFu.
For this reason the group is cyclic of order two. Since KS contains i a primitive 4-th root of unity KSd is a cyclic extension of KS. Albert has exhibited a non-cyclic division algebra of characteristic zero with index 4 having a pure maximal subfield.
If is a local field an algebraic number field or more generally a global field then every central division algebra over F is cyclic. It is one of the most. Cyclic algebras were on a large scale first studied by DicksonJ 2 3 Kap.
Cyclic algbras Given a nite cyclic extension Kkwith galois group generated by and an element a2k de ne the cyclic algebra Kka as the quotient of the twisted polynomial algebra Kx bx xb for b2K by the two-sided ideal. I 3 42 in particular stated the following criterion. A normal division algebra D of degree n over R is a cyclic algebra 1 D Z S y and has a basis 2 ij - 1 where zi z is a basis of the cyclic field Z over R with generating automorphism S.
A space-time codebook is obtained via the standard F-embedding of Dinto. Cyclic generations and related concepts. Instead of normal division algebras.
Here are two examples. Classifying or even nding non-commutative division algebras is a di cult task. A general example of cyclic division algebra is given based on a construction of Brauer yielding examples of division algebras of arbitrary prime exponent without proper central subalgebras and also noncrossed products of arbitrary exponent.

Abstract Algebra 1 Definition Of A Cyclic Group Youtube Cyclic Group Binary Operation Algebra 1

How To Solve Cyclic Expressions Example 1 Maths Algebra Youtube
Http Www Cs Fsu Edu Hawkes Ft Chap2 Poly Sp06 Pdf

Cyclic Groups A Cyclic Group Is A Group Which Can Be Generated By One Of Its Elements That Is For Some A In G G A N N Is An Element Of
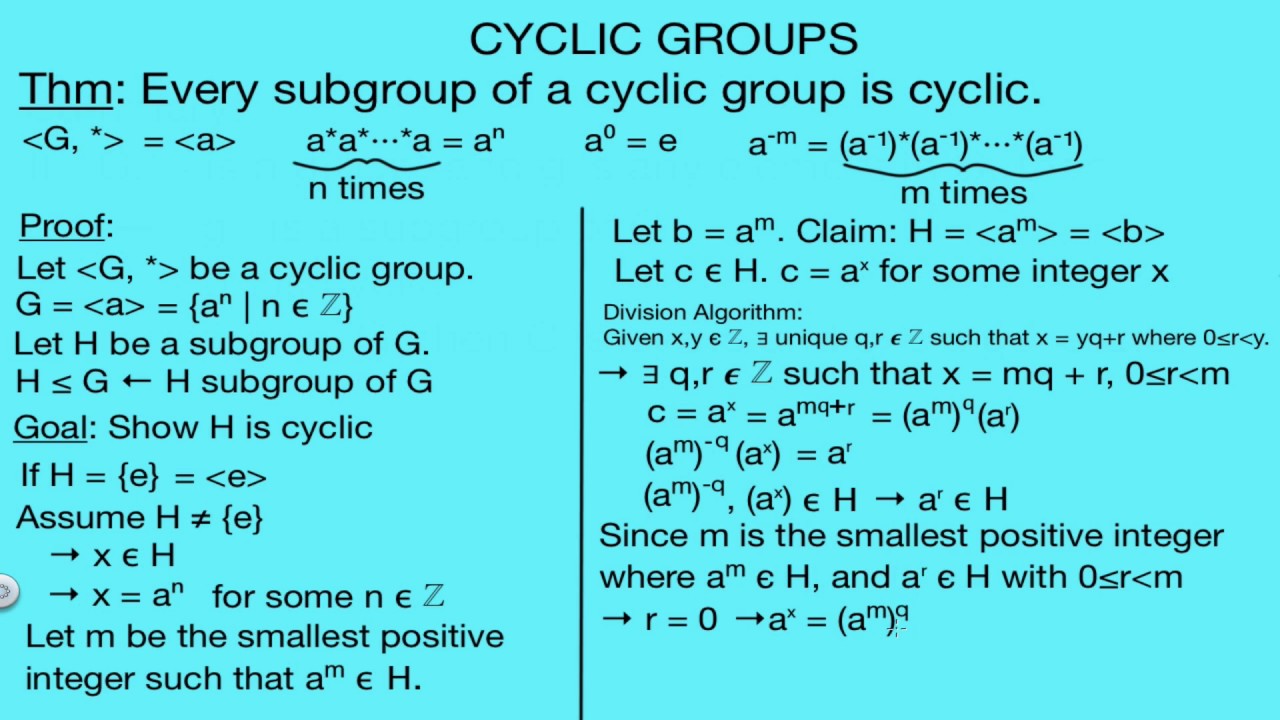
Every Subgroup Of A Cyclic Group Is Cyclic Proof Youtube

Show Z 0 Forms A Cyclic Group Under Multiplication Modulo 5 Z 0 Doesn T Under Modulo 6 Youtube
Cyclic Division Algebras A Tool For Space Time Coding Caltechauthors

Is The Group Of Units Of A Finite Ring Cyclic Mathematics Stack Exchange
Https Www Ams Org Journals Tran 1931 033 01 S0002 9947 1931 1501586 7 S0002 9947 1931 1501586 7 Pdf

Proof Subgroup Of A Cyclic Group Is Cyclic Sumant S 1 Page Of Math
Https Projecteuclid Org Journals Pacific Journal Of Mathematics Volume 3 Issue 1 Finite Multiplicative Subgroups In Division Rings Pjm 1103051509 Pdf

Cyclic Redundancy Check And Modulo 2 Division Tutorialspoint Dev

Ma136 2015 2016 Lecture Notes 10 Cyclic Groups And Cyclic Subgroups Studocu

Simple Cyclic Group Proof Mathematics Stack Exchange
Https Www Jstor Org Stable 1989507
Tutorial 14 The Family Tid Of Idempotent Chords

